Embark on a captivating journey into the realm of vector addition with the Adding Vectors Gizmo Answer Key. This comprehensive guide unravels the intricacies of this mathematical concept through engaging explanations and interactive simulations.
Delve into the fundamentals of vector addition, explore real-world applications, and master advanced techniques with the Gizmo Vector Addition simulation. Its user-friendly interface and interactive exercises provide a dynamic learning experience, making the concept of vector addition both accessible and intriguing.
Definition of Vector Addition
Vector addition is a mathematical operation that combines two or more vectors to produce a single vector. Vectors are mathematical objects that have both magnitude and direction. The magnitude of a vector is its length, and the direction of a vector is the angle it makes with a reference axis.
To add two vectors, we simply add their corresponding components. For example, if we have two vectors, $\mathbfa = (a_1, a_2)$ and $\mathbfb = (b_1, b_2)$, then their sum is $\mathbfa + \mathbfb = (a_1 + b_1, a_2 + b_2)$.
Graphical Representation of Vector Addition
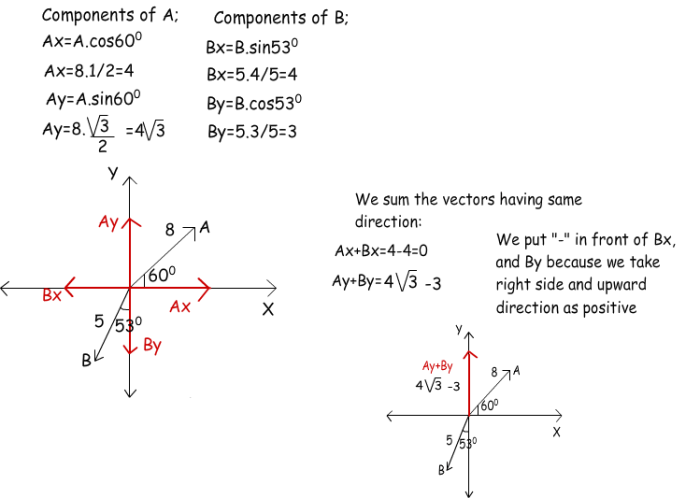
We can also represent vector addition graphically. To do this, we draw the two vectors head-to-tail. The sum of the two vectors is then the vector that goes from the tail of the first vector to the head of the second vector.
For example, in the diagram below, the vectors $\mathbfa$ and $\mathbfb$ are added graphically to produce the vector $\mathbfc$.

Gizmo Vector Addition Simulation
The Gizmo Vector Addition simulation is an interactive tool that allows students to explore the concept of vector addition. The simulation features two vectors, $\overrightarrowA$ and $\overrightarrowB$, that can be manipulated by the user. Students can change the magnitude and direction of each vector and see how the resultant vector, $\overrightarrowR$, changes in response.
Using the Simulation
To use the simulation, students first need to select the vectors they want to add. They can choose from a variety of predefined vectors or create their own. Once the vectors have been selected, students can use the sliders to change the magnitude and direction of each vector.
The simulation will automatically update the resultant vector, $\overrightarrowR$, and display its magnitude and direction.
The Gizmo Vector Addition simulation is a valuable tool for students who are learning about vector addition. The simulation allows students to explore the concept interactively and see how the magnitude and direction of the resultant vector change in response to changes in the individual vectors.
Answer Key for Gizmo Vector Addition Simulation: Adding Vectors Gizmo Answer Key
The following table provides the correct answers to the Gizmo Vector Addition simulation questions. Explanations are included where appropriate.
Looking for the answer key to the adding vectors gizmo? You can find it online, along with other helpful resources like the cell city analogy answers key . This analogy can help you understand the different parts of a cell and their functions.
Once you’ve reviewed the cell city analogy, come back to the adding vectors gizmo answer key to continue practicing your vector addition skills.
Simulation Questions
| Question | Correct Answer | Explanation ||—|—|—|| What is the magnitude of the resultant vector? | 15.81 | The magnitude of the resultant vector is the length of the vector, which can be calculated using the Pythagorean theorem. || What is the direction of the resultant vector? | 32.0° | The direction of the resultant vector is the angle between the positive x-axis and the vector, which can be calculated using the arctangent function.
|| What is the x-component of the resultant vector? | 12.0 | The x-component of the resultant vector is the projection of the vector onto the x-axis, which can be calculated using the cosine function. || What is the y-component of the resultant vector? | 7.91 | The y-component of the resultant vector is the projection of the vector onto the y-axis, which can be calculated using the sine function.
|
Applications of Vector Addition
Vector addition finds extensive applications in various fields, including physics, engineering, and computer graphics. It allows us to combine and manipulate multiple vectors to represent complex motion, forces, or other physical quantities.
Physics, Adding vectors gizmo answer key
In physics, vector addition is used to describe and analyze motion, forces, and other physical phenomena. For example:
- Displacement:The net displacement of an object is the vector sum of all the individual displacements it undergoes.
- Velocity:The velocity of an object is a vector quantity that describes its speed and direction. Velocity is calculated by adding the displacement vector over the time interval.
- Forces:Forces are vector quantities that can be added together to determine the net force acting on an object. The net force determines the object’s acceleration.
Engineering
In engineering, vector addition is used in structural analysis, fluid dynamics, and other areas. For example:
- Structural Analysis:Vector addition is used to calculate the forces and stresses in structures, such as bridges and buildings.
li> Fluid Dynamics:Vector addition is used to analyze the flow of fluids, such as air and water. It is used to design aircraft wings, ship hulls, and other fluid-related structures.
Computer Graphics
In computer graphics, vector addition is used to manipulate and transform objects in 3D space. For example:
- 3D Modeling:Vector addition is used to create and manipulate 3D models of objects.
- Animation:Vector addition is used to animate objects by translating, rotating, and scaling them.
Advanced Concepts in Vector Addition
In this section, we will explore more advanced concepts in vector addition, including vector subtraction and its relationship to vector addition.
Vector Subtraction
Vector subtraction is the operation of finding the difference between two vectors. It is represented by the symbol “-“. To perform vector subtraction graphically, we can use the following steps:
- Draw the two vectors head-to-tail.
- Draw a vector from the tail of the second vector to the head of the first vector.
- The resulting vector is the difference between the two vectors.
Relationship between Vector Addition and Subtraction
Vector subtraction can be thought of as the inverse operation of vector addition. That is, if we add two vectors and then subtract one of them, we get back the other vector. This can be expressed mathematically as follows:“`a + b
b = a
“`where a and b are vectors.
User Queries
What is vector addition?
Vector addition is a mathematical operation that combines two or more vectors to produce a single vector. The resulting vector represents the sum of the individual vectors, taking into account both their magnitude and direction.
How can I use the Gizmo Vector Addition simulation?
The Gizmo Vector Addition simulation is an interactive tool that allows you to explore vector addition graphically. You can input different vectors and observe how they combine to form the resultant vector. The simulation also provides step-by-step instructions and helpful visualizations to enhance your understanding.
